Difference between revisions of "Lattices"
KevinYager (talk | contribs) |
KevinYager (talk | contribs) (→Cubic) |
||
| Line 29: | Line 29: | ||
There are three [http://en.wikipedia.org/wiki/Cubic_crystal_system cubic] space groups: | There are three [http://en.wikipedia.org/wiki/Cubic_crystal_system cubic] space groups: | ||
* [[Lattice:Simple_cubic|Simple cubic (SC)]] | * [[Lattice:Simple_cubic|Simple cubic (SC)]] | ||
| − | ** [[Lattice: | + | ** [[Lattice:Simple_cubic#Alternating_Simple_Cubic|Alternating simple cubic (NaCl)]] |
* [[Lattice:BCC|Body-centered cubic (BCC)]] | * [[Lattice:BCC|Body-centered cubic (BCC)]] | ||
** [[Lattice:BCC#Body-centered_Two-particle|CsCl]] | ** [[Lattice:BCC#Body-centered_Two-particle|CsCl]] | ||
Revision as of 17:52, 13 November 2016
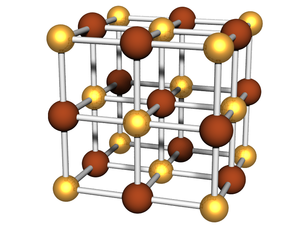
In x-ray scattering, we frequently study materials which have constituents arranged on a well-defined lattice. For instance, an atomic crystal has atoms which occupy well-defined sites within a representative unit cell, which then repeats in all three directions throughout space. Nanoparticle superlattices are a nanoscale analogue, where each lattice site is occupied by a nanoparticle. Other kinds of nanostructures systems can be considered similarly. Block-copolymer mesophases can be thought of as nanostructures sitting on lattice sites (e.g. cylinders in a hexagonal lattice).
Well-defined realspace lattices (repeating structures) give rise to well-defined peaks in reciprocal-space, which makes it possible to determine the realspace lattice by considering the arrangement (symmetry) of the scattering peaks.
Contents
Notation
- Real space:
- Crystal planes:
- (hkl) denotes a plane of the crystal structure (and repetitions of that plane, with the given spacing). In cubic systems (but not others), the normal to the plane is [hkl]
- {hkl} denotes the set of all planes that are equivalent to (hkl) by the symmetry of the lattice
- Crystal directions:
- [hkl] denotes a direction of a vector (in the basis of the direct lattice vectors)
- denotes the set of all directions that are equivalent to [hkl] by symmetry (e.g. in cubic system 〈100〉 means [100], [010], [001], [-100], [0-10], [00-1])
- hkl denotes a diffracting plane
- Crystal planes:
- Reciprocal space:
- Reciprocal planes:
- [hkl] denotes a plane
- denotes the set of all planes that are equivalent to [hkl]
- Reciprocal directions:
- (hkl) denotes a particular direction (normal to plane (hkl) in real space)
- {hkl} denotes the set of all directions that are equivalent to (hkl)
- hkl denotes an indexed reflection
- Reciprocal planes:
Lattices
Cubic
There are three cubic space groups:
There are many conceptually distinct lattices that exhibit one of the above cubic symmetries:
- Diamond lattice (FCC)
Hexagonal
Symmetry and Space Groups
- U. Shmueli, S. R. Hall and R. W. Grosse-Kunstleve, Symmetry in reciprocal space International Tables for Crystallography Volume B: Reciprocal space, 1, Springer 2001 pp 99-161 ISSN 1574-8707 ISBN 978-0-7923-6592-1 (Print) 978-1-4020-5407-5 (Online) doi 10.1107/97809553602060000552