Example:P3HT orientation analysis
This tutorial describes how to quantify the orientation distribution of the semiconducting polymer P3HT using GIWAXS. This orientation analysis is meant to determine the relative amounts of the material oriented in different ways. The same kind of analysis can be applied to other semiconducting polymers or small-molecules. In fact, the same conceptual steps can be applied more broadly to determining any kind of orientation distribution (though one must be careful in interpreting the relationship between reciprocal-space peaks, which will be different for each material's specific unit cell).
Contents
P3HT orientation
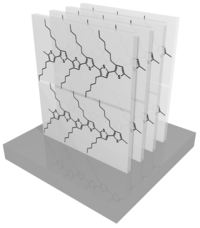
P3HT crystallizes into the unit cell shown below. P3HT crystals are anisotropic, often appearing as long needle-like structures. Note that this unit cell is highly idealized: the alkyl side-chains have considerable freedom and thus disorder (they may even be liquid-like). Moreover, real samples of P3HT organize in a more disordered state than shown here. Although the lamellar stacking is well-defined, and the aromatic (π-π) stacking is also well-defined, one typically does not observe any scattering peak along the backbone direction: i.e. there is usually no well-defined persistence of order in this direction. It is also likely that subsequent chains do not organize with the well-defined registry shown in the cartoon. Overall, P3HT is thus better thought of as being semi-crystalline or liquid-crystalline: it exhibits considerable molecular order (giving rise to scattering peaks), but is not an extended well-ordered crystal.
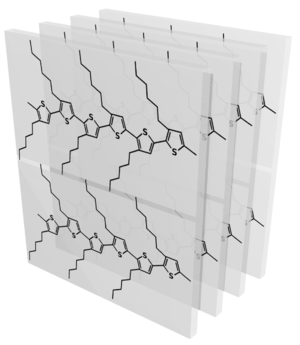
- The lamellar stacking has a spacing of ~1.6 nm, giving rise to a peak (100) at q ~0.4 Å−1.
- The aromatic (π-π) stacking has a spacing of ~0.39 nm, giving rise to a peak (010) at q ~1.6 Å−1.
- The spacing along the ring direction is too disordered to give a well-defined 001 peak.
When P3HT is cast as a thin-film, this unit cell can adopt a variety of orientations. Although most materials form 3D powders when cast from solution, P3HT adopts a relatively well-defined orientation with respect to the substrate. It seems that the alkyl side-chains preferentially segregate to the film-air and film-substrate interfaces (presumably in order to lower the interfacial energy), which drives the material overall into the edge-on orientation shown below:
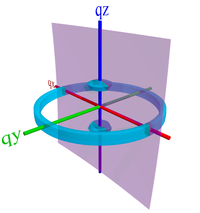
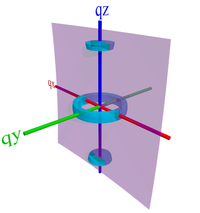
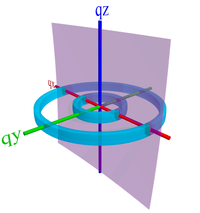
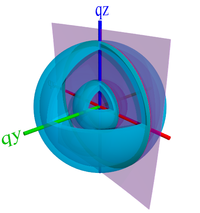
Absent any other driving force, the above configurations are assumed to be in-plane isotropic (2D powders). In such a case, one would expect to see reciprocal-spaces corresponding to these states of:
Of course, what one observes on the detector is only where the Ewald sphere intersects reciprocal-space:
Summarizing:
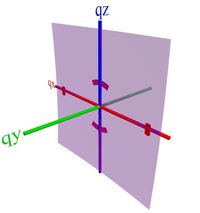
- Edge-on involves the lamellar side-chains wetting the interfaces, which means the lamellar stacking is vertical (100 peak along qz), and the π-π stacking is then in-plane (010 peak along qr).
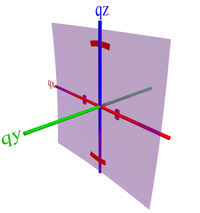
- Face-on involves the aromatic rings facing the substrate, which means the lamellar stacking is in-plane (100 peak along qr), and the π-π stacking is in the film normal direction (010 peak along qz).
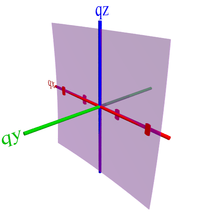
- End-on involves the chain ends pointing towards the substrate, which means the lamellar stacking is in-plane (100 peak along qr), and the π-π stacking is also in-plane (010 peak along qr). Since the chain axis doesn't give a well-defined peak, there is no scattering along qz.
- Isotropic involves a complete orientational averaging of the unit cell orientation. The lamellar (100) peak and the π-π (010) peak will both appear to be rings of uniform intensity.
Example GIWAXS
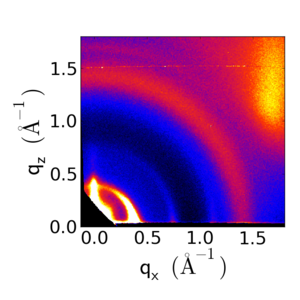
Shown below is a typical GIWAXS image of P3HT cast on a silicon substrate:
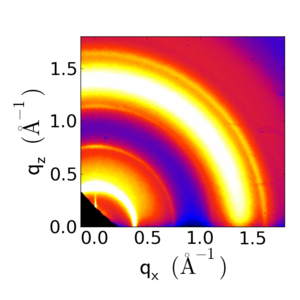
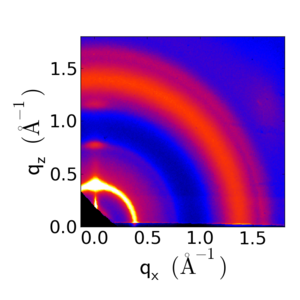
Because of the edge-on orientation, the lamellar peaks appear along the qz axis. Below is a comparison of P3HT with different orientation distributions.
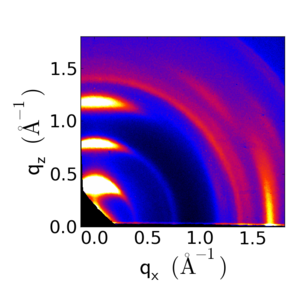 P3HT with predominantly edge-on orientation. The 100 peak is along qz, while the 010 peak is along qx. |
Analysis: In-plane powder
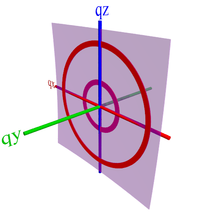
In order to quantify the orientation distribution of P3HT, we need to measure the intensity of the scattering as a function of angle. We define the azimuthal angle to be χ: this is the angle with respect to the qz axis. I.e. χ = 0° is the out-of-plane (qz) axis, while χ = 90° is the in-plane (qr) axis.
Step 1: Conversion to q-space
The raw detector image needs to be converted into reciprocal-space. This is typically done by using a calibration standard, which has rings at known q-position. The purpose of calibration is to convert from pixel position to value. One needs to know:
- The x-ray wavelength. This is known since it is set by the x-ray source (and/or monochromator).
- The unitless detector distance D/d, where D is the detector distance and d is the detector width. Since d is typically known, one can either measure D directly (even using a tape measure is reasonably accurate), or by noting the pixel position of a ring in calibration standard.
- Direct beam position (i.e. the pixel position of the direct beam). Even with the beam blocked by a beamstop, low-q beam spillover is usually sufficient to note the beam position. One can also determine the center of scattering rings to define the beam position.
- Detector tilt. This can be assessed by noting the curvature of scattering rings from a standard sample.
With the above information, one can convert from the raw image into data in reciprocal-space (various pieces of software will do this for you).
Notice that one can either display the data as or as , where:
The representation ignores the qy component of the momentum transfer. For small-angle measurements (GISAXS), this is a reasonable approximation. However for wide-angle (GIWAXS) measurements, this is a poor approximation: the curvature of the Ewald sphere means that the part of reciprocal-space probed by the detector is curving away from the plane. As such, in the representation, we note a 'missing wedge' of data near the qz axis. In fact, in grazing-incidence geometry, we do not probe the true qz axis, except at two points (the direct beam position, and the specularly-reflected beam position).
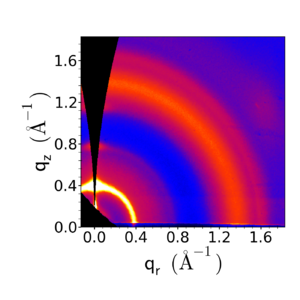 Data converted to q-space, taking into account the Ewald sphere. |
The conversion to q-space is necessary for all subsequent analysis steps. Moreover, we typically are interested in χ defined in reciprocal-space (i.e. with respect to the sample coordinates, not the instrument reference frame), so we should compute χ in the representation shown above.
Step 2: Linecut
From the converted data, we can take a linecut along a χ-arc. In the present analysis, the most useful place to take such a cut is along the 100 lamellar peak (and then along the 010 aromatic stacking peak). When taking the linecut, one should consider:
- When extracting the intensities along the arc, one should try to integrate the full peak width. The integration must be wide enough to take the full peak into account for all χ (otherwise the intensity will change along χ simply due to the fraction of the peak one is probing.
- The intensity data should be background-subtracted. In this case, subtracting the local background makes the most sense: i.e. subtract the intensity just outside the arc of interest. (This must be done at each corresponding χ, since the background may not be isotropic.)
- The χ-scale should be shifted in order to take into account the above-noted curvature of the Ewald sphere. Thus, there will be a small gap in the data near χ = 0°.
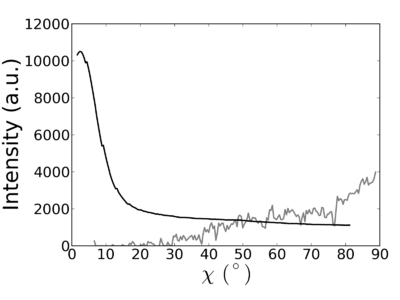
- One should ignore the Yoneda streak, since it exhibits an intensity enhancement. Any data at χ beyond the Yoneda should also be discarded since this data comes from below the horizon, and is thus attenuated. For the P3HT 100 peak, this usually means eliminating χ > ~82°.
- In principle, one should re-adjust the χ-scale to take into account refraction distortions: the grazing-incidence geometry induces substantial beam refractions, which causes reciprocal-space to look warped on the detector image. This distortion only affects the qz component, and is greatest near the Yoneda. This distortion is substantial in GISAXS, but is usually negligible in GIWAXS.
Step 3: Account for sample symmetry
The I vs. χ curve shown above can be thought of as the orientation distribution of the P3HT. However, one must be careful in directly interpreting the intensity as representing the amount of material. The reason for this (as usual) is that the Ewald sphere is probing only a single slice through the 3D reciprocal-space. So we are not probing the full scattering intensity for any given population.
How to properly account for the full scattering intensity depends on sample symmetry. In the most general sense, we can rotate the sample, accumulate multiple images, and reconstruct the full 3D reciprocal-space. However, it is far easier to account for this mathematically, if we know the sample symmetry. It turns out, that for an in-plane powder, we must simply multiply the above curve by . For a detailed explanation of why this is the case, refer to integrated intensity. Roughly, this factor arises from the spherical coordinate system, aligned with the symmetry axis of the 2D powder. More heuristically, one can imagine that observed scattering intensity near qr actually represents a whole ring of scattering in the 3D reciprocal-space. This 'ring' becomes smaller at larger χ; the factor exactly accounts for this variation.
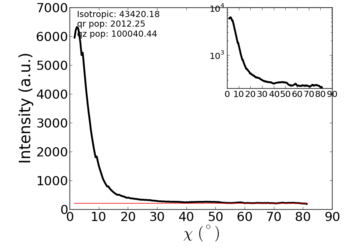
|
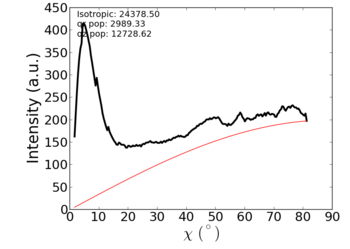
|
The corrected data (right panel above) now has the intensity being proportional to the amount of material oriented at that χ angle. This curve can be reported as an orientation distribution for the material (closely related to pole figures).
Step 4: Integrate populations
One can now integrate the intensity in the corrected curve, to come up with estimates of the relative amount of material. There are many ways one could choose to do this. In this example, we divide the scattering intensity into three populations:
- Isotropic: The scattering intensity arising from the subset of grains that form an isotropic distribution.
- Edge-on: The scattering intensity arising from the edge-on grains. We include all grains with an orientation χ<45°.
- Face-on: The scattering intensity arising from the face-on grains. We include all grains with an orientation χ>45°.
Note that we are here assuming that all the intensity from the 100 scattering along qr arises from entirely from face-on material. However, both face-on and end-on material would give rise to scattering at that position in reciprocal-space. To differentiate between those two possibilities, one must invoke additional data. Specifically, one can look at the 010 (π-π) peak: for end-on, the π-π peak will also be in-plane (along qr), whereas for face-on, one should observe substantial intensity of the π-π peak in the out-of-plane direction (near qz axis).
For the present example, the end-on orientation was excluded as a possibility, and therefore we ascribe all of the qr scattering to the face-on orientation. We compute integrated quantities by summing up the area under the curve, and distributing it into the three categories noted above. Importantly, the isotropic population appears as a uniform baseline (isotropic ring) in the original data, and thus appears as a baseline in the corrected data.
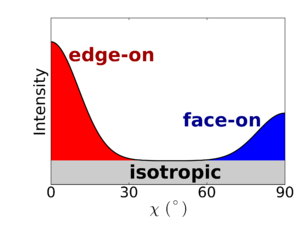
|
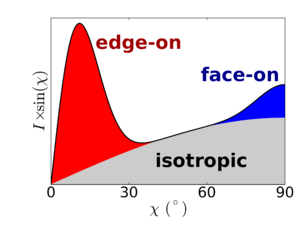
|
Note again that only the intensities in the corrected curve (right panel above) are linearly representative of the amount of material. We can compare the three integrated values to the total, and thereby compute a percentage for edge-on, face-on, and isotropic.
Analysis: In-plane aligned
Note that for a sample that isn't an in-plane powder (e.g. P3HT aligned in a grating), then the above symmetry arguments would change. In that case, one would need to instead account for the orientation distribution in the in-plane direction (ϕ). Note that if the material were highly aligned with the grating axis ((ϕ = 0°), then a single measurement in this aligned geometry would be sufficient to assess the full orientation distribution. In other words, the original uncorrected data would correctly represent the relative amounts of material:
See also grating alignment for caveats related to the in-plane angle (ϕ).
Literature
Development/description of analysis method
- Nanoimprint-Induced Molecular Orientation in Semiconducting Polymer Nanostructures Htay Hlaing, Xinhui Lu, Tommy Hofmann, Kevin G. Yager, Charles T. Black, and Benjamin M. Ocko ACS Nano 2011, 5 (9), 7532-7538 doi: 10.1021/nn202515z
- Enhanced charge collection in confined bulk heterojunction organic solar cells Jonathan E. Allen, Kevin G. Yager, Htay Hlaing, Chang-Yong Nam, Benjamin M. Ocko and Charles T. Black Applied Physics Letters 2011, 99, 163301. doi: 10.1063/1.3651509 c.f. Supplementary Information
- One-Volt Operation of High-Current Vertical Channel Polymer Semiconductor Field-Effect Transistors Johnston, D.E.; Yager, K.G.; Nam, C.-Y.; Ocko, B.M.; Black, C.T. Nano Letters 2012, 8, 4181–4186 doi: 10.1021/nl301759j
- Nanostructured Surfaces Frustrate Polymer Semiconductor Molecular Orientation Johnston, D.E.; Yager, K.G.; Hlaing, H.; Lu, X.; Ocko, B.M.; Black, C.T. ACS Nano 2014 doi: 10.1021/nn4060539
Application of method
- Stable and Controllable Polymer/Fullerene Composite Nanofibers through Cooperative Noncovalent Interactions for Organic Photovoltaics Fei Li, Kevin G. Yager, Noel M. Dawson, Ying-Bing Jiang, Kevin J. Malloy, and Yang Qin Chemistry of Materials 2014 doi: 10.1021/cm501251n
- Nano-structuring polymer/fullerene composites through the interplay of conjugated polymer crystallization, block copolymer self-assembly and complementary hydrogen bonding interactions Fei Li, Kevin G. Yager, Noel M. Dawson, Ying-Bing Jiang, Kevin J. Malloyc and Yang Qin Polymer Chemistry 2015 doi: 10.1039/C4PY00934G
Related papers
Angular correction (curvature of Ewald sphere)
- Quantification of Thin Film Crystallographic Orientation Using X-ray Diffraction with an Area Detector Jessy L. Baker, Leslie H. Jimison, Stefan Mannsfeld, Steven Volkman, Shong Yin, Vivek Subramanian, Alberto Salleo, A. Paul Alivisatos and Michael F. Toney Langmuir 2010, 26 (11), 9146-9151. doi: 10.1021/la904840q
- Simulating X-ray diffraction of textured films D. W. Breiby, O. Bunk, J. W. Andreasen, H. T. Lemke and M. M. Nielsen J. Appl. Cryst. 2008, 41, 262-271. doi: 10.1107/S0021889808001064
sin(angle) correction
- Confinement-Driven Increase in Ionomer Thin-Film Modulus Kirt A. Page, Ahmet Kusoglu, Christopher M. Stafford, Sangcheol Kim, R. Joseph Kline, and Adam Z. Weber Nano Letters 2014, 14 (5), 2299-2304. doi: 10.1021/nl501233g
Other orientation analyses
- Evaluation of equatorial orientation distributions C. Burger and W. Ruland J. Appl. Cryst. 2006, 39, 889-891. doi: 10.1107/S0021889806038957
- Two-dimensional small-angle X-ray scattering of self-assembled nanocomposite films with oriented arrays of spheres: determination of lattice type, preferred orientation, deformation and imperfection W. Ruland and B. M. Smarsly J. Appl. Cryst. 2007, 40, 409-417. doi: 10.1107/S0021889807010503
- Device-Scale Perpendicular Alignment of Colloidal Nanorods Jessy L. Baker, Asaph Widmer-Cooper, Michael F. Toney, Phillip L. Geissler and A. Paul Alivisatos Nano Letters 2010, 10 (1), 195-201. doi: 10.1021/nl903187v
- A systematic approach for quantitative orientation and phase fraction analysis of thin films through grazing incidence X-ray diffraction